概率论与数理统计第五章：大数定理和中心极限定理

知识点

5.1 大数定律

• 切比雪夫不等式

  设随机变量 具有期望 ,方差 ,则对于任的正数,有

• 概率收敛

  设 是一个随机变量序列， 是一个常数。若对于任意正数 ，有，则称序列 依概率收敛于 ，记为 。

• 切比雪夫大数定律

  设 是相互独立的随机变量序列，每一随机变量都存在有限的方差，且一致有界，即存在常数 ，使得 ，。则对任意的 ，有

  该定律说明充分大时个独立随机变量的平均数的离散程度小

• 伯努利大数定律

  设是重相互独立重复试验(即伯努利试验)中事件出现的次数，而 是事件 A 在每次试验中出现的概率，则对任意的正数,有

  该定律说明随机事件的频率在概率附件摆动

• 辛钦大数定律

  如果{}是相互独立同分布的随机变量序列，其数学期望 ,则对任意给定的 ,有

  该定律说明：对独立同分布的随机变量序列，只要验证数学期望是否存在，就可判定其是否服从大数定律.

5.2 中心极限定理

• 独立同分布的中心极限定理

  设 是相互独立同分布的随机变量序列，且 ,,则对 ,有

• 棣莫弗-拉普拉斯中心极限定理

设随机变量 表示 重伯努利试验中事件 发生的次数是事件 在每次试验中出现的概率，则对任意实数,有

习题

• 用切比雪夫不等式估计概率

  ​​

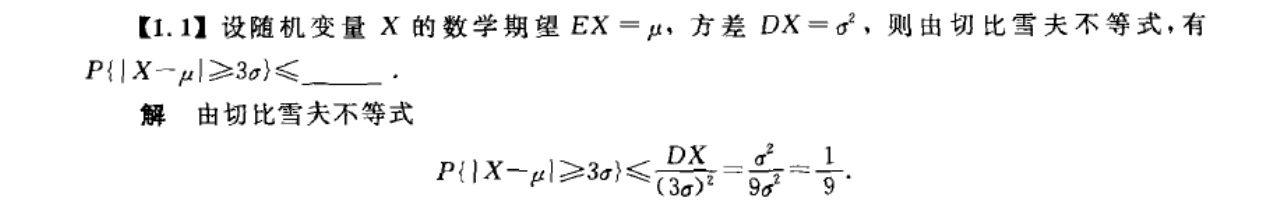
• 大数定律的应用

  ​​

• 判断是否符合辛钦大数定律（检查数学期望是否存在且有限即收敛）

  ​​

• 利用中心极限定理求概率

  ​​

  ​​

‍