概率论与数理统计第七章：参数的点估计及其优良性

知识点

点估计

设是总体的未知参数，用统计量来估计，称为的估计量.对于样本的一组观察值 ,代人的表达式中所得的具体数值称为 的估计值.这样的方法称为参数的点估计。

矩估计法

矩估计法是一种用样本矩去估计相应总体矩，或者用样本矩的函数去估计总体矩的同一函数的估计方法。

设总体 的概率分布有 个未知参数 。假定总体的 阶原点矩存在，记为 ，其中 。

样本的 阶矩定义为 。

令总体的 阶矩等于样本的 阶矩，即

解这个方程组得到的解 称为参数 的矩估计量。矩估计量的观察值称为矩估计值。

最大似然估计

1. 似然函数的定义：

   设总体 的概率分布为 ，其中 是未知参数。当 为连续型随机变量时， 是概率密度函数；当 为离散型随机变量时， 是分布律。

   对于给定的样本观察值 ，似然函数定义为：

2. 最大似然估计值和估计量：

   对于给定的样本观察值 ，使似然函数 达到最大值的参数值 称为 的最大似然估计值。

   相应地， 称为 的最大似然估计量，其中 表示随机样本。

3. 最大似然估计的求解方法：

   由于 与 有相同的最大值点，且计算 更方便，通常对 进行求导并令导数为零来寻找最大值点。即解

• 有时求导等于零会失效，即似然函数驻点不存在，此时可以通过参数的取值范围求最大似然

点估计优良性的评定标准

1. 无偏性

   设为来自总体 的 样 本 , 为 的 一 个 估 计 量 , 如 果 成立，则称估计量为参数 的无偏估计

2. 有效性

   设都为参数 的无偏估计量，若 ,则称 比 有效
   特别地，若对于的任一无偏估计,有

   则称是的最小方差无偏估计 ( 最佳无偏估计 ) .

3. 一致性（相合性）

   设为未知参数 的估计量，若对任意给定的 ,都有

   即依概率收敛于参数 ,则称为 的一致估计或相合估计.

习题

求矩估计

1. 连续型分布求矩估计

   ​​

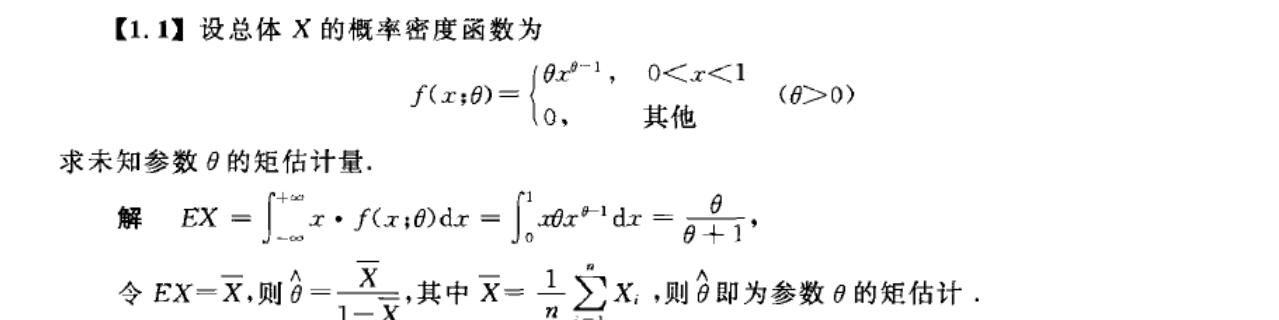
2. 离散型分布求矩估计

   ​​

求最大似然估计

1. 驻点法

   ​​

2. 参数范围法

   ​​

无偏性问题

​​

有效性问题

1. 先验证无偏性，再比较有效性

   ​​

2. 证明在的无偏估计量中,为最有效的估计

   ​​

‍