概率论与数理统计第四章:随机变量的数字特征
知识点
4.1 随机变量的数学期望
离散型随机变量的期望定义
设离散型随机变量
的分布律为 若级数 绝对收敛,则称 为随机变量
的数学期望,若级数 不收敛,则称 的数学期望不存在.数学期望也称为平均值、均值。 连续型随机变量的期望定义
设连续型随机变量
的密度函数为 ,若积分 收敛,则称 为随机变量
的数学期望。 一维随机变量函数的数学期望
设
是随机变量 的函数,即 ,其中 是连续函数。 若
是离散型随机变量,其分布律为 ( ),且 绝对收敛,则随机变量 的数学期望存在,且 若
是连续型随机变量,其概率密度为 ,且 绝对收敛,则
二维随机变量函数的期望
设
是随机变量 和 的函数,即 ,其中 为连续函数。 当
为二维离散型随机变量,其分布律为 若 则随机变量 且
设
且
期望的性质
- 若随机变量
4.2 方差
方差的定义
设
称
离散型随机变量的方差:
连续型随机变量的方差:
方差的计算:
方差的性质
- 若
- 若
- 若随机变量
- 若
4.3 常见分布的随机变量的期望与方差
常见离散型分布
0-1分布
设
二项分布
设
泊松分布
设
几何分布
设
常见连续型分布
均匀分布
设
指数分布
设
正态分布
设
4.4 协方差和相关系数
协方差定义
设
协方差的性质
对称性:
若
若
随机变量和的方差与协方差的关系:
相关系数定义
由于协方差不能很好地量化两个变量的关系强度,协方差的绝对值越大并不直接意味着相关程度越强,因为它还取决于变量的尺度。因此引入相关系数
设
为随机变量
相关系数的性质
当
当
当
如果
设 二 维 随 机 变 量
令
, 、 随机变量的标准化
设随机变量
- 对任何一个随机变量有
- 设
- 对任何一个随机变量有
4.5 矩和协方差矩阵
矩
原点矩
设
特别地,当
显然,随机变量
中心矩
设随机变量
特别地,当
当
显然,随机变量
协方差矩阵
设
- 协方差矩阵为对称矩阵
- 协方差矩阵为半正定矩阵
习题
期望
求离散型随机变量的期望
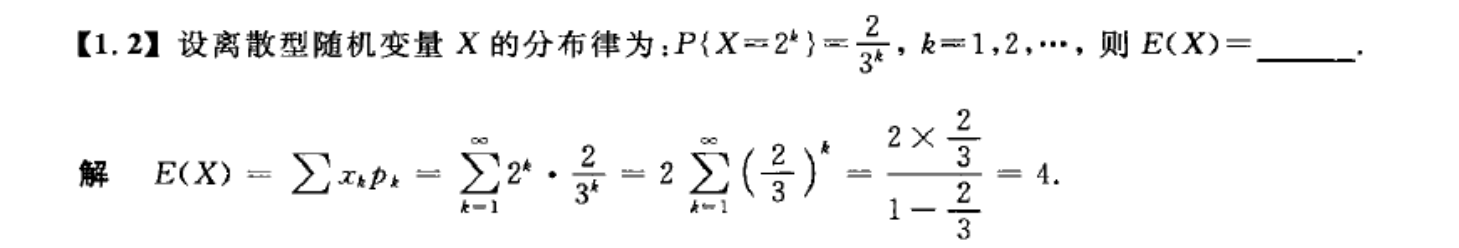
求连续型随机变量的期望

求离散型二维随机变量函数的期望

求连续型二维随机变量函数的期望

利用性质求期望


利用对称性证明期望
例:设随机变量
方差
方差的计算

期望和方差的综合运用
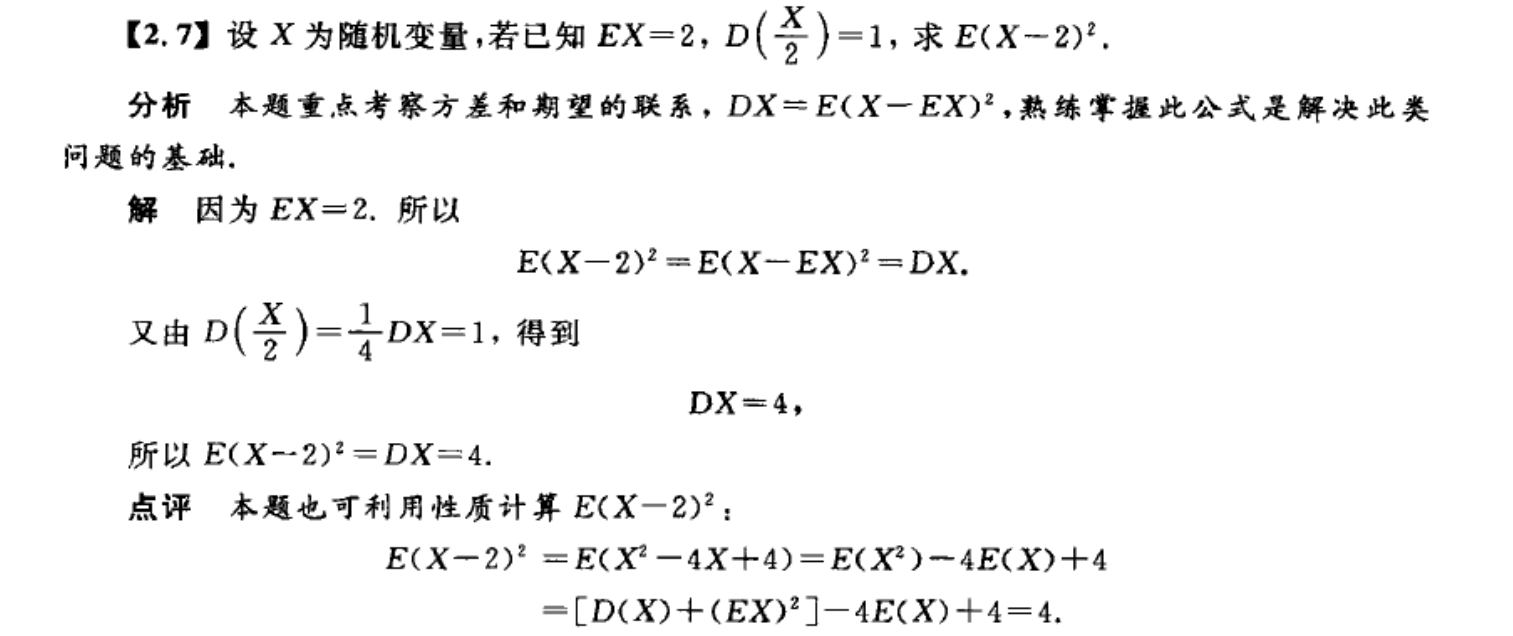
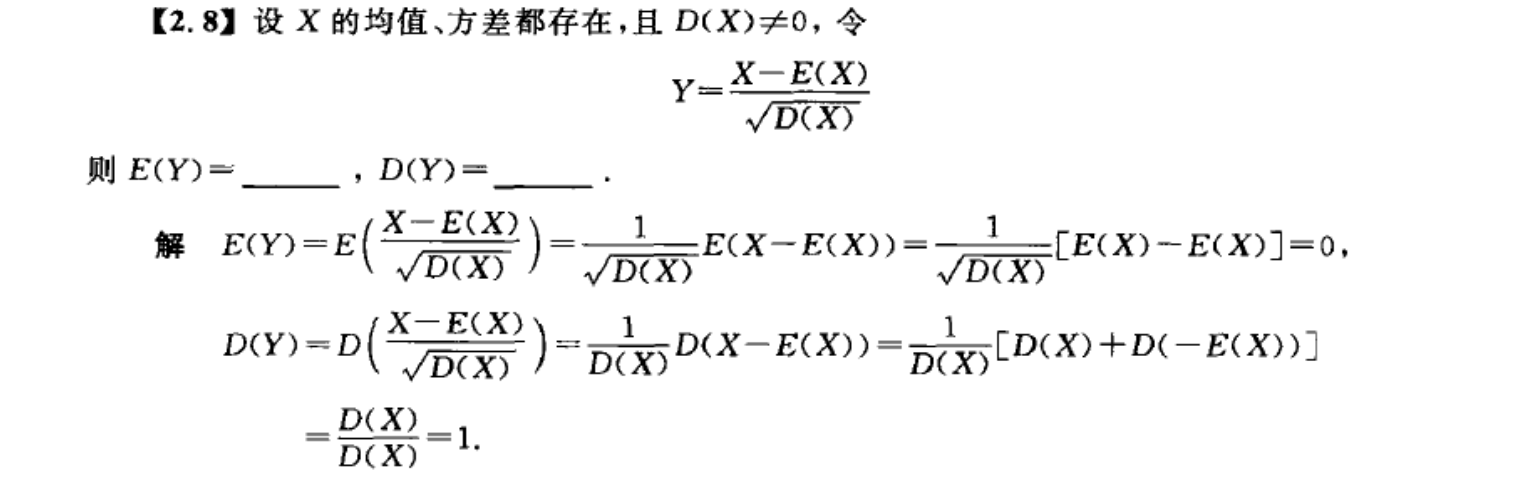
协方差和相关系数
计算矩和协方差矩阵

性质
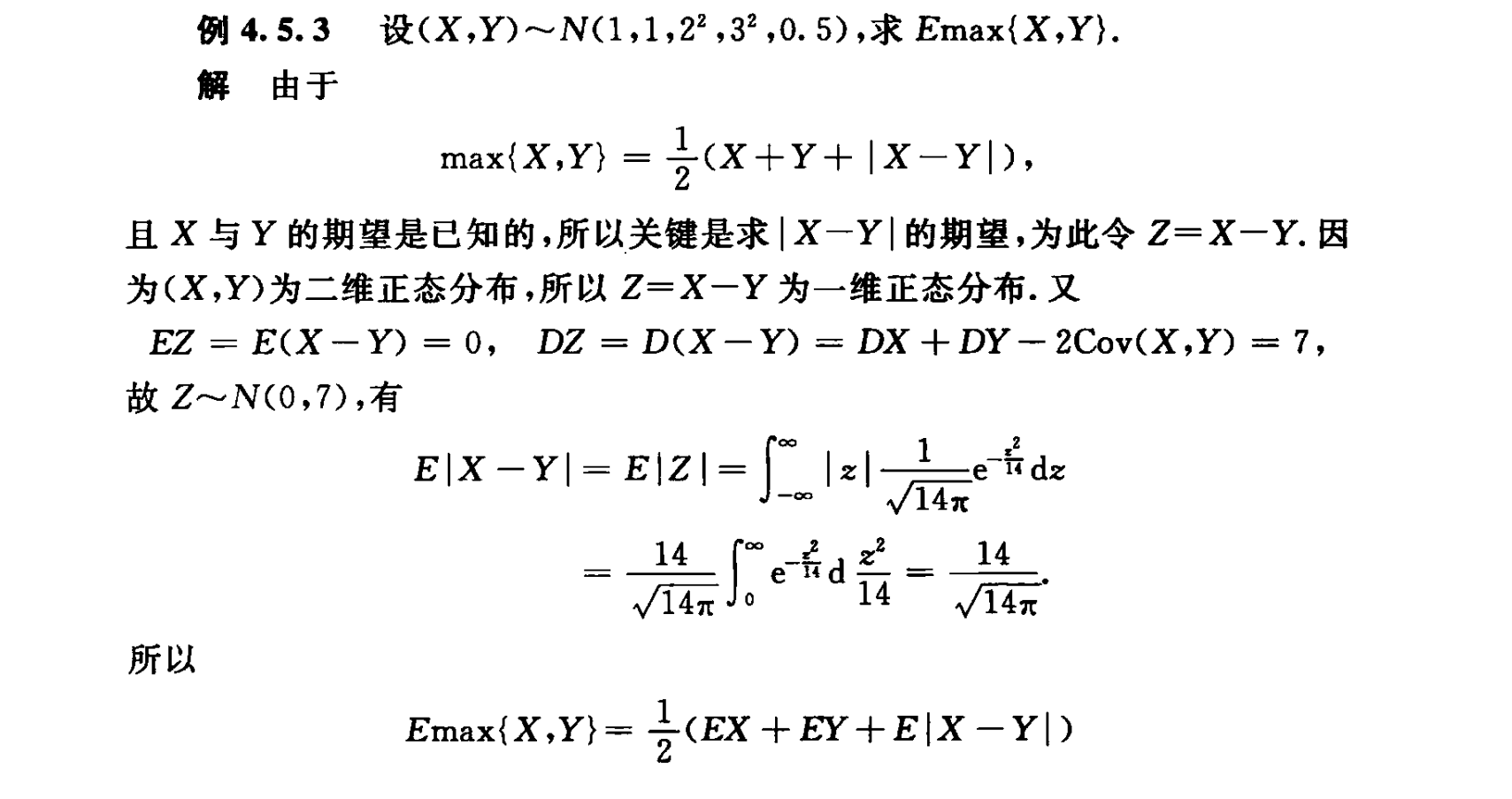




请输入一个邮箱再评论。
如果您在 Gravatar 注册过邮箱,将显示您的 Gravatar 头像;否则将随机显示一个默认头像。
您可以在 Gravatar 注册并设置自己的头像。