概率论与数理统计第六章:数理统计基本概念
知识点
6.1 总体、样本、统计量
总体 :是指研究对象的某个性能指标的全体,通常用一随机变量
或 的分布 代表总体 个体: 是指每一个研究对象.
样本: 从总体中取
个个体, 为样本容量,这部分个体称为样本 简单随机样本是指
个相互独立,而且与总体 同分布的随机变量 ,简称随机样本,也常以随机向量( )表示,它们的一组观察值 称为样本值(样本观测值). 设总体
的分布函数为 ,概率密度函数为 ,则样本 的联合分布函数为 ,联合概率密度函数为 统计量: 称不含未知参数的样本函数
为统计量 - 样本均值:
- 样本方差:
,除以n-1是为了实现样本方差对总体方差的无偏估计 - 样本标准差:
- 样本
- 极大次序统计量:
- 极小次序统计量:
- 样本均值:
6.2 常见统计量的分布
服从自由度为
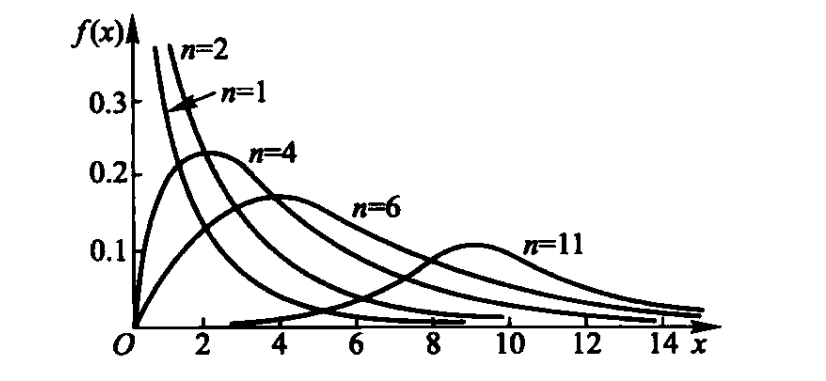
Γ函数:
- 设
设随机变量
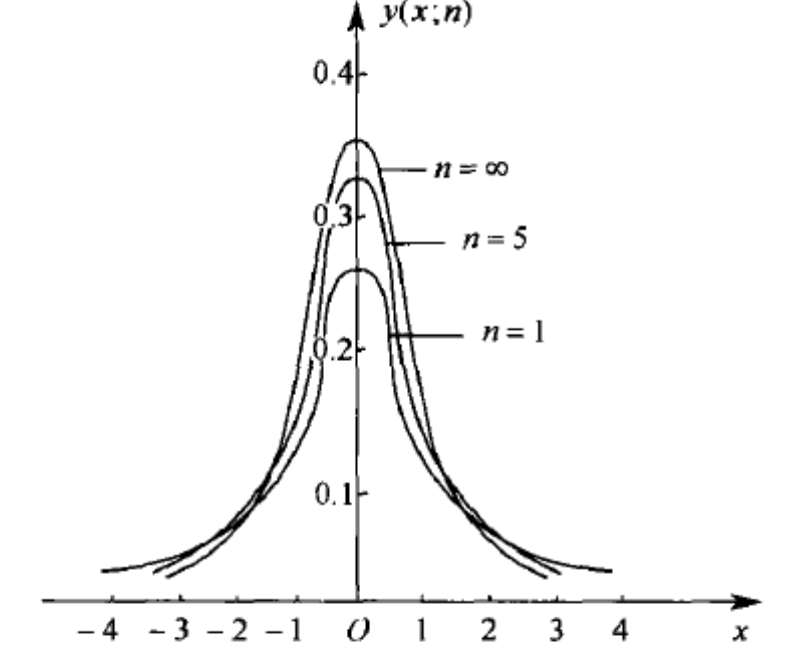
设随机变量
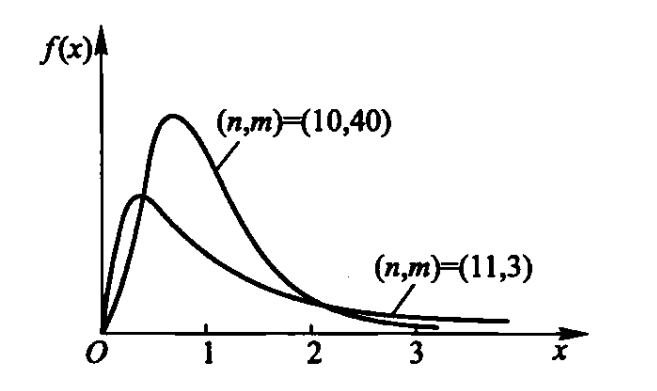
- 若
- 若
- 若
6.3 正态总体的抽样分布
单正态总体的抽样分布定理
设总体
且
双正态总体的抽样分布定理
设总体
当
其中,
6.4 抽样分布的上
标准正态分布的
设随机变量
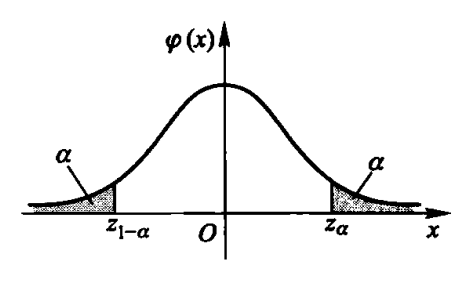
设随机变量
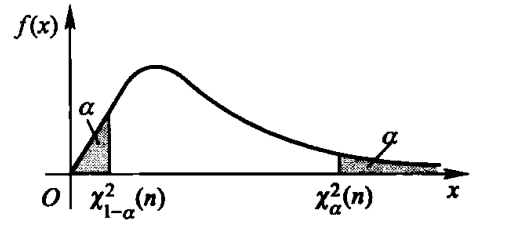
设随机变量
实 数
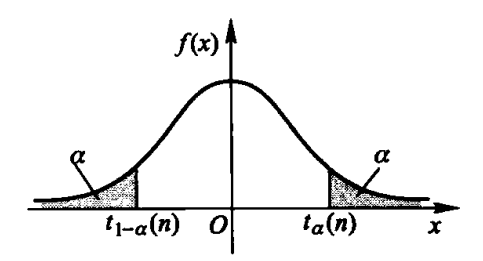
设随机变量
实 数
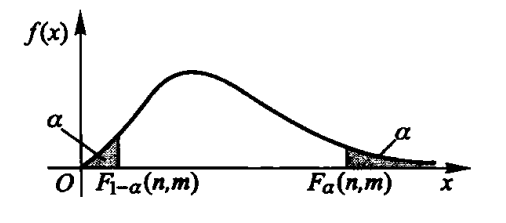
设
满 足 则 称 点 为 或
习题
判断抽样分布的类别


统计量求数字特征

关于分位点

统计量的综合应用


请输入一个邮箱再评论。
如果您在 Gravatar 注册过邮箱,将显示您的 Gravatar 头像;否则将随机显示一个默认头像。
您可以在 Gravatar 注册并设置自己的头像。