知识点

2.1 随机变量及其分布函数

定义

设为一个样本空间，若对,都有一个实数与之对应，则称为一个上的随机变量，并简记为。一般地随机变量用大写字母 $、、、$ 表示。

随机变量就是一个由样本空间到实轴的映射，即样本空间数字化

分为：
1. 随机试验结果本身是数字
2. 随机试验结果是数组、面积或其他
随机变量的分布函数

设为一个随机变量，我们称为随机变量的分布函数。
性质
1. 为的右连续函数，所以分区间时等号在左边如
2. 为的单调不减函数

2.2 离散型随机变量

定义

如果随机变量的所有可能取值为一列离散的点 ,则称为一个离散型随机变量，并称概率$ P(X=x_i)=p_ii=1,2, $为$ X$的分布列或分布律。分布列也常常可以写成下列的形式：
性质
1. 离散型随机变量的分布函数必为阶梯函数（充要条件）
2. 非负性
3. 归一性
二项分布

设为一个离散型随机变量，若的分布列为

$。$

其中，,则称服从参数为与的二项分布，记为

二项分布，就是在重独立重复试验中事件发生的次数的分布
泊松（Poisson）分布

设为一个离散型随机变量，若的分布列为

其中，,则称服从参数为的泊松分布,记为
泊松逼近定理

设,常数,如果,则有
几何分布

设为一个离散型随机变量，若的分布列为

其中，,则称服从参数为的几何分布,记为
几何分布的无记忆性

若是服从参数为的几何分布，则
超几何分布

设为一个离散型随机变量，若的分布列为

其中，,则称服从参数为的超几何分布,记为

2.3 连续型随机变量

定义

设为一个随机变量,如果存在一个函数使得的分布函数满足，则称为一个连续型随机变量，并称 ) 为的概率密度函数，简称密度函数
性质
1. 非负性，
2. 归一性，
3. 在密度函数的连续点处有
4. 连续型随机变量的分布函数必为连续函数，反之不一定成立
均匀分布

若随机变量的密度函数为 $其他$ 则称在区间上服从均匀分布，记为，分布函数为
指数分布

若随机变量的密度函数为 $，$ ，则称服从参数为的指数分布，记为，分布函数为

指数分布也是无记忆性的，即

几何分布看作是第一次命中的等待次数，而指数分布是等待某个事件首次发生的等待时间
正态分布

若随机变量的密度函数为 $，，$ ，则称服从参数为的正态分布，记为

时的正态分布称为标准正态分布，密度函数为，分布函数为

若，令，则转化为

2.4 随机变量函数的分布

2.4.1 离散型随机变量函数的分布

若是离散型随机变量，其分布列为

,显然也是离散型随机变量，则的分布列为

$。$

2.4.2 连续型随机变量函数��分布

若为连续型随机变量，已知的密度函数为,,若也为连续型随机变量，则求的密度函数的一般步骤为：

由的取值范围，根据,确定的取值范围 .
在内求的分布函数,此分布函数是一个积分函数形式.
对的分布函数求导，即得的密度函数.

习题

泊松分布取特殊值问题

设随机变量服从参数为的泊松分布，试求取偶数的概率。

$为偶数，为奇数$

所以 $为偶数为奇数$ ，又因为 $为偶数为奇数$

所以 $为偶数$

泊松分布最大值

设随机变量，我们需要找到使概率最大的值，以及最大��是多少。

通过计算，我们可以得到以下结论：

当时，，即。
当时，，即。

因此，当不是整数时，最大概率出现在，即的整数部分。当是整数时，最大概率出现在和。当时，最大概率出现在。

已知分布列求分布列

已知的分布列为，其中。我们需要求的分布列。

当取正整数时，的所有可能取值为。我们可以计算出：

已知密度函数求密度函数

设随机变量服从区间上的均匀分布，即。

求 的密度函数：

对两侧求��，有。由于，因此，且 $其他$ 。
求 的密度函数：

对两侧求导，有。由于，因此，且 $其他$ 。

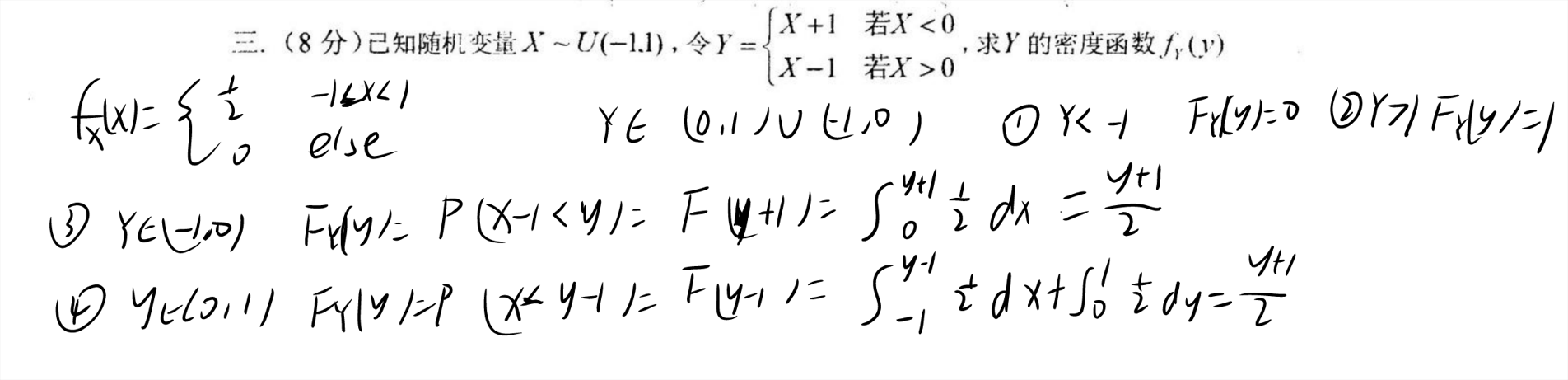
密度函数中反函数的应用

设为连续型随机变量的密度函数，且严格单调增加，求的密度函数。

解由于为分布函数，所以随机变量的取值范围为,

当时， ;当时， ;

当时，由于严格单调增加，所以的反函数存在，于是

$。$

所以的密度函数为

$其他。$

二项分布取最大

已知，��当为何值时，最大。

，。，将标准化，即转化为标准正态分布：

令，则服从标准正态分布。因此，

其中，为标准正态分布的累积分布函数。由于标准正态分布的累积分布函数关于轴对称，因此当时，取得最大值。因此，当时，最大。

概率论与数理统计第二章：随机变量及其分布

知识点