知识点

3.1 二维随机变量的联合分布与边际分布

  • 二维随机变量的定义：

    设 和 为 上的两个随机变量，则称有序数组 为 上的二维随机变量。

  • 联合分布函数定义

    设 为一个二维随机变量，对任意实数 ，定义二元函数：为 的联合分布函数。

    在点 处的函数值表示随机点 落在以 为顶点且位于其左下方的无穷矩形域上的概率。

  • 联合分布函数性质

    1. 对 或 都是不减函数。

    2. ，，，

    3. 分别对 和 右连续。即：和

    4. 矩形法则：即落在以为顶点的矩形的概率

      对任意 和 ，有：

  • 边际分布函数

    单个随机变量的分布称为边际分布，比如 的分布函数 称为 的边际分布函数。

    联合分布函数 与其边际分布函数的关系：

    由联合分布可得边际分布，但反之不成立

3.2 二维离散型随机变量

  • 二维离散随机变量的定义：

    设 和 为 上的两个离散随机变量，则称 为 上的二维离散随机变量。

  • 二维离散随机变量的联合分布列或联合分布律：

    此时联合分布函数为：

  • 离散型随机变量的边际分布

    为的边际分布列，记作

    为 的边际分布列，记作

    联合分布列可决定边际分布，但反之不成立

  • 二维离散随机变量的独立性定义

    如果对任意的,都有 则称 与 是相互独立。

  • 条件概率

    称 为已知的条件下的分布列

    称 为已知的条件下的分布列

3.3 二维连续型随机变量

  • 定义

    设 为二维随机变量 的联合分布函数，若存在非负函数,使得对于任意的 ,有

    则称为二维连续型随机变量，并称 为的联合概率密度函数 , 简称联合密度(或概率密度)

  • 在 的连续点处有

    如果 是二维连续随机变量，那么与 肯定都是一维连续随机变量，反之不成立

  • 边际密度函数为：

    ，

  • 二维均匀分布

    设 为平面有界闭区域，其面积为 ,若密度函数为则称二维随机变量服从上的二维均匀分布.

  • 二维正态分布

    二维正态分布的联合概率密度函数可以表示0为

    ${1}>0 ,{2}>0 ,||<1 ，记为(X,Y){}N(_1,_2,_1^2,_2^2,)$

    特殊的，当，时，，当时，

  • 二维正态分布的两个边缘分布都是一维正态分布

    ，

  • 二维连续随机变量的独立性

    若或则称随机变量 和 是相互独立的.

  • 二维正态分布相互独立的充要条件是

  • 二维连续随机变量的条件密度

    条件分布函数：，

    条件密度函数：，

3.4 二维随机变量函数的分布

  • 二维离散随机变量函数的分布

    image

  • 二维连续随机变量函数的分布

    image

  • 极大极小分布

    设随机变量 相互独立，且 的分布函数为 ，其中 。令 ，。那么有：

    1. 的分布函数为 。
    2. 的分布函数为 。

  • 正态分布的可加性：设随机变量相互独立，且,那么对于任意常数,2, 及常数,有

    。

习题

  • 判断是否为联合分布函数

    image

  • 已知联合分布函数求边际分布

    image

  • 已知联合密度函数求边缘密度

    image

  • 求离散型随机变量的边际分布

    image

  • 已知二维连续随机变量联合分布求密度函数

    image

  • 已知密度函数求概率

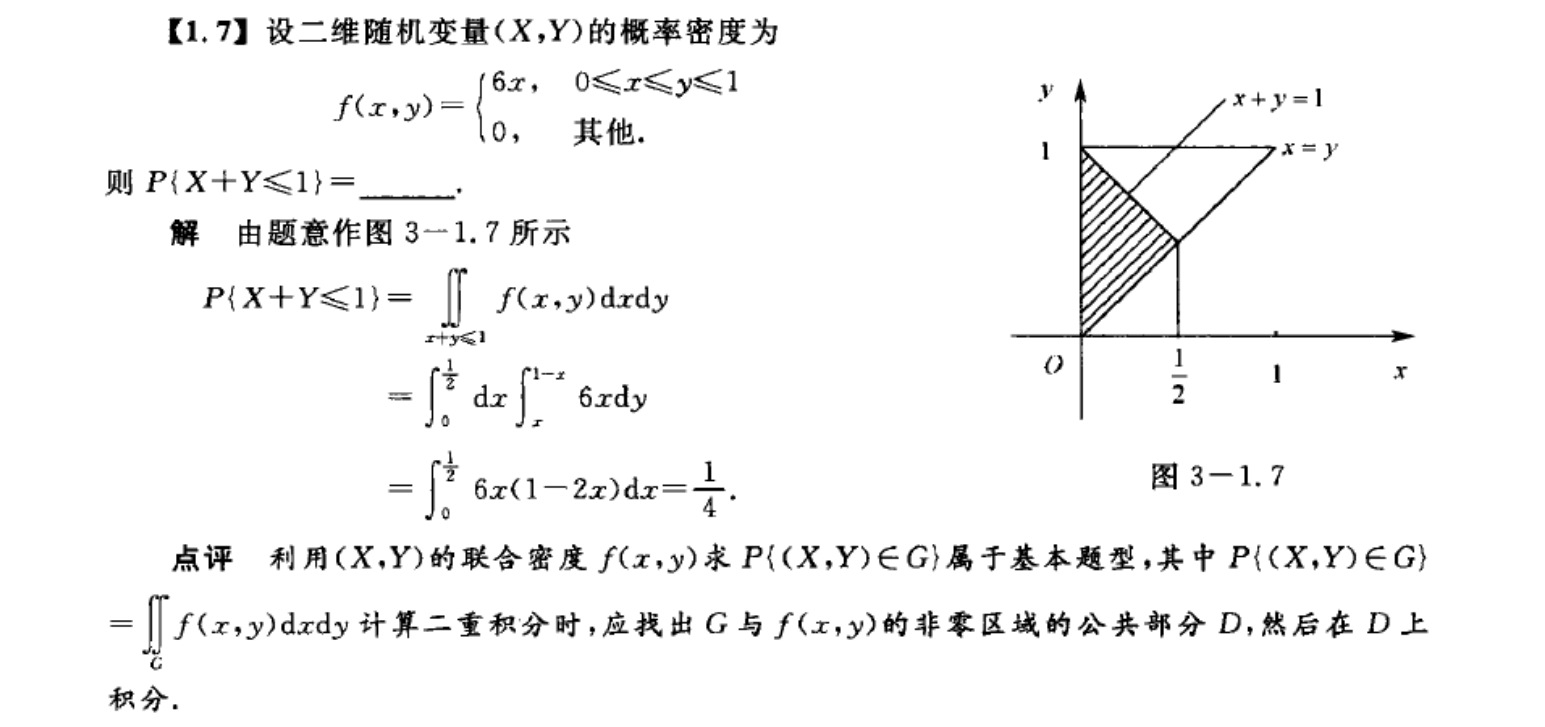
    image

  • 求条件密度函数

    image

  • 型函数的分布

    ![image]/images/image-20240927085136-cr21ek7.png)

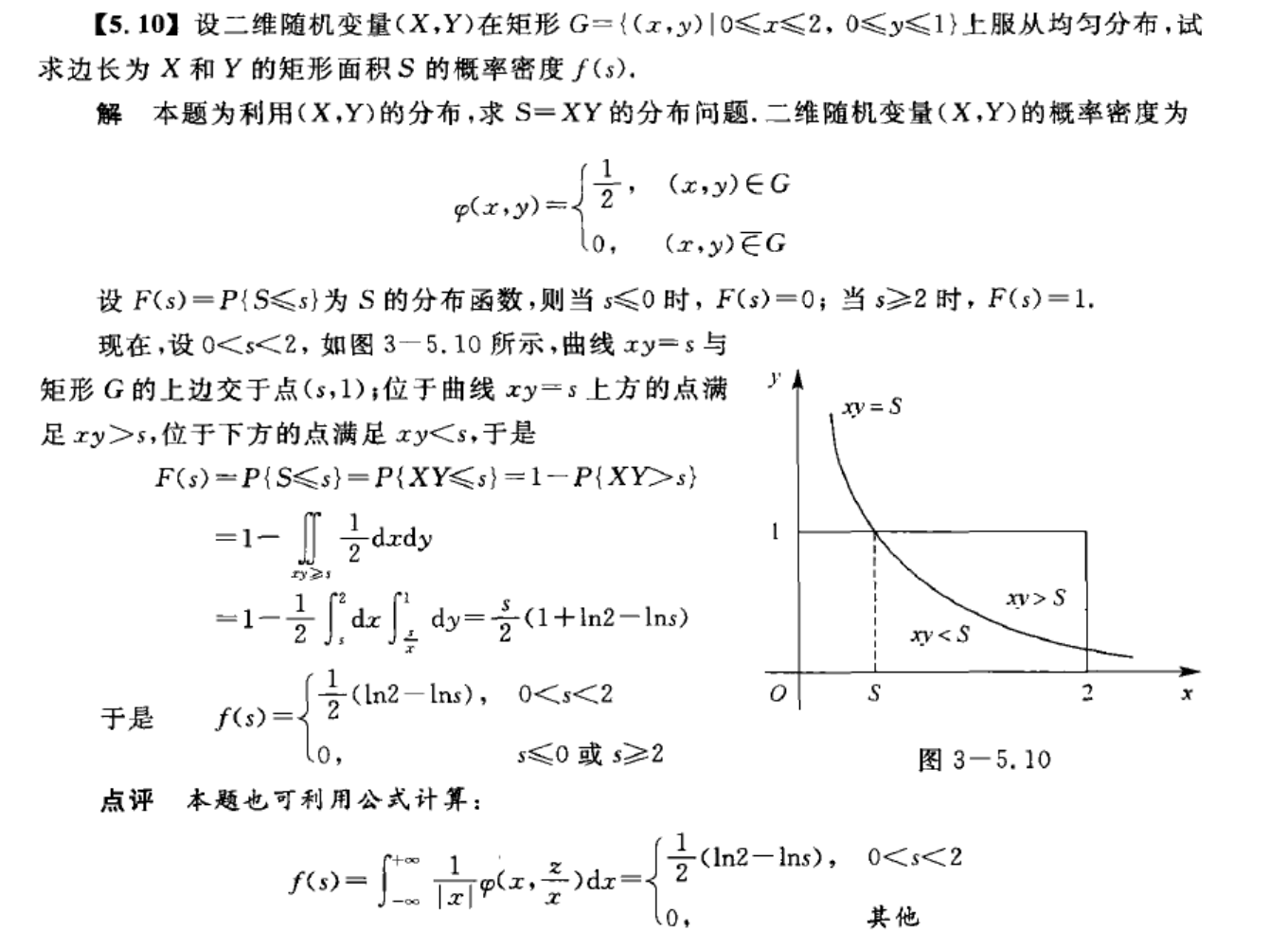
    image

  • 型函数的分布

    image

  • 型函数的分布

    image

  • 电路问题

    image

  • 极大极小分布问题

    设随机变量 相互独立，且 （）服从区间 上的均匀分布。定义 和 ，求随机变量 和 的概率密度函数。

    对于随机变量 ，我们有：

    其他

    对于随机变量 ，我们有：

    其他