基本知识点

1.1 随机事件及其运算

  • 随机现象（或随机试验）的定义

    一个现象E如果满足以下三个特征，我们就称该现象为一个随机现象（或随机试验）：

    1. 可重复性：该试验可以在相同条件下重复进行。
    2. 可预测性：所有可能出现的结果是已知的。（可列的）
    3. 不确定性：试验结果的出现具有随机性

    对于随机试验E，我们用符号表示其所有可能结果组成的集合，记作 ，这个集合被称为随机试验E对应的样本空间。样本空间中的元素被称为样本点，即样本点就是随机试验的可能结果。

  • 随机事件：随机试验 E 对应的样本空间 的子集

  • 必然事件：样本空间 自身；不可能事件：空集
    必然事件概率一定为1，但概率为1不一定是必然事件，不可能事件同理（用几何概型可证明：打到靶心概率为0但并非不可能发生）

  • 事件的关系与运算

    1. 事件的包含与相等：如果事件A的每一个样本点都包含在事件B中，则称事件B包含事件A，记为或。如果且，则称事件A与B相等，记为。
    2. 和事件：设A与B为两个随机事件，事件称为A与B的和事件，有时也记为。它表示A或B至少有一个发生的事件。对于n个事件，它们的和事件表示至少有一个发生，记为。
    3. 积事件：设A与B为两个随机事件，事件称为A与B的积事件，有时也记为​。它表示A和B同时发生的事件。对于n个事件，它们的积事件表示所有事件都发生，记为。
    4. 差事件：设A与B为两个随机事件，事件称为A与B的差事件。它表示A发生而B不发生的事件。注意
    5. 补事件：设A为随机事件，事件称为A的补事件。它表示A不发生的事件。
    6. 互不相容：如果，则称A与B互不相容或互斥。这意味着A和B不能同时发生。

  • 事件运算和的一些重要原则：

    1. 交换律：

      • ，

    2. 结合律：

    3. 分配律：对于任意事件 和事件集合 ，有以下等式成立：

    4. De Morgan 法则：

      • ，
      • 记忆方法：德摩根​

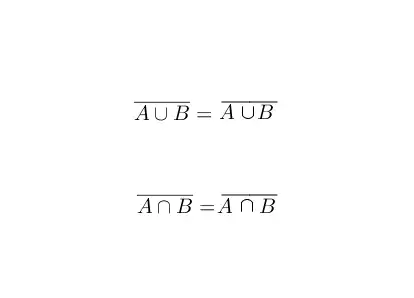
1.2 概率的定义及其基本性质

  • 定义

    设为随机试验E的样本空间。对于任意事件，如果存在一个实数与之对应，并满足以下条件：

    1. 非负性：，即概率值非负；

    2. 归一性：，即样本空间的概率为1；

    3. 可列可加性：设是一列两两互不相容的事件，即对于所有，则事件的并集的概率等于这些事件概率的和，即

    则称为事件的概率。

  • 性质

    1. ，证明：

    2. 可列可加性取即可证明有限可加性：

      设是个两两互不相容的事件，则有

    3. 如果，则，证明：，但若严格包含于却不能证明

    4. ​

    5. 减法公式：。

    6. 加法公式：
      ​，
      ​

1.3 等可能概型

1.3.1 古典概型

  • 排列组合

    1. 排列：从给定的n个元素中取出r个元素，按照一定的顺序进行排列。计算公式为
    2. 组合：从给定的n个元素中取出r个元素，不考虑元素的顺序。计算公式为：

  • 定义

    当一个随机试验满足一下两个条件时，我们称该试验对应的概率模型为古典概型。

    1. 有限性：样本空间中的样本点总数是有限的。
    2. 等可能性：每个样本点出现的可能性相同。

  • 在古典概型中，事件的概率可以用以下公式计算：

    事件中样本点的数量样本点总数

  • 摸球问题

    设有 个不同的球，要从中任取 个球

    1. 有放回摸球：每次摸球后，将球放回原位，然后再进行下一次摸球。这种情况下，每次摸球时，都有N个球可供选择，因此样本点总数为。
    2. 不放回摸球，但与次序无关：每次摸球后，不将球放回原位，但我们只关心摸出的球的组合，而不关心它们的顺序。这种情况下，样本点总数为从N个球中选择n个球的组合数，样本点总数为表示
    3. 不放回摸球，且与次序有关：每次摸球后，不将球放回原位，且我们关心摸出的球的顺序。样本点总数为

    • 例：设袋中有6个白球和4个红球，共10个球。

      1. 有放回摸球，求5个球中恰有3个白球的概率：
      2. 不放回摸球，求5个球中恰有3个白球的概率：
      3. 不放回摸球，求5个球中第三个球为白球的概率（先取一个白球）：

  • 分房问题

    • 例 ：将 n个人随机分到 N 个房间中去，,每个人分到哪个房间时等可能的，且假设每个房间可容纳的人数没有限制，求

      1. 某指定的一个房间(比如第一个房间)恰有个人的概率。：
      2. 每两个人都不在同一个房间的概率：

  • 抽签问题

    例：设有 15 个人要去看电影，只有 7 张电影票，于是进行抽签决定谁去 看电影。求第 5 个人抽到电影票的概率：

    抽签与顺序无关

  • 分组法

    将个不同的球分成个不同的组,使得每组各有个球，总的取法为：

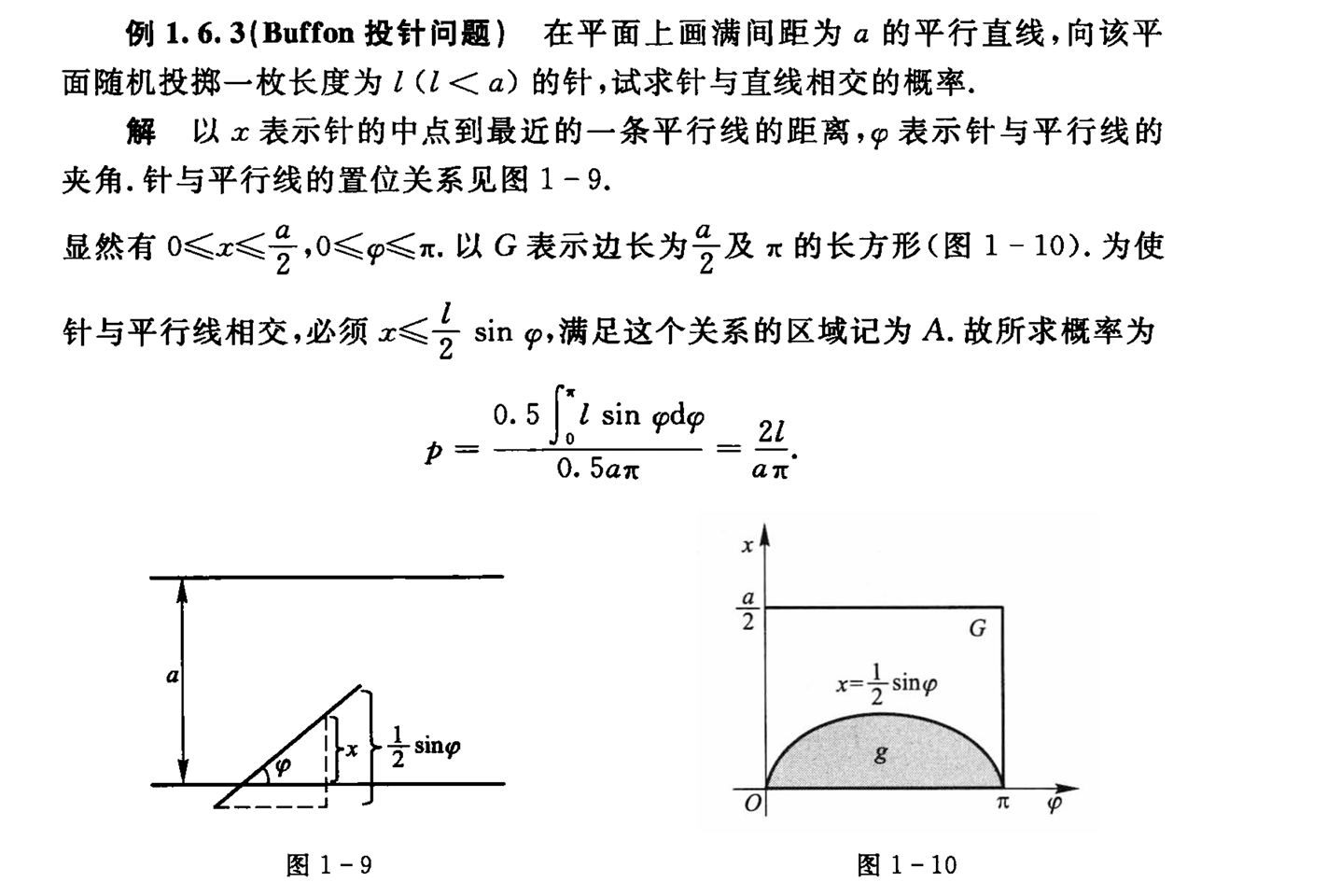
1.3.2 几何概型

  • 定义

    几何概型具有以下两个特征：

    1. 无限性：实验中所有可能出现的基本事件（结果）有无限多个。
    2. 等可能性：每个基本事件出现的可能性相等。

  • 计算

    在几何概型中，如果我们有一个可以度量的区域G，其中包含一个子区域g，那么随机选择一个点落在g中的概率可以定义为：

    的测度的测度

    其中，测度可以是长度、面积或体积，具体取决于问��的性质。

  • 会面问题

    ​image​

1.4 条件概率

  • 条件概率定义

    设 A 与 B 为两个事件，且。那么在“已知事件 发生”的条件下，事件的条件概率定义为

  • 条件概率性质

    1. 非负性：对任意事件 ,有
    2. 归一性：
    3. 可列可加性：对任意的一列两两互不相容的事件,有

  • 乘法公式

  • 样本空间的划分（分割、完备事件组）

    设为一组事件，如果且则称是的划分（分割、完备事件组）

  • 全概率公式（关键在于构造第一阶段事件的划分）

    设为的一组划分，则对任意的事件 B,有

    全概率公式应用范围：在第一阶段所有可能已知且第一阶段的试验结果对第二阶段有影响的时候求第二个阶段结果的概率

  • 贝叶斯公式

    设 是 的一个划分，如果 ,则对任意事件 B,只要,就有

    称为先验概率，条件概率称为后验概率

1.5 独立性与贝努利试验

1.5.1 独立性

  • 相互独立定义

    设 A 与 B 为两个事件，如果等式成立则称事件 与 相互独立：

  • 相互独立性质

    1. 若且 与 相互独立，则，即独立必相交，互斥则必不独立
    2. 若事件 A 与 A 独立，则 或
    3. 在这四对事件中,如果有一对独立,则另外三对也独立

  • 多个事件的相互独立定义

    为 个事件,从中任取的个事件 均满足则称相互独立

    相互独立的定义包括两两独立但两两独立不能推出相互独立

1.5.2 伯努利试验

在次独立重复试验中，如果事件在每次试验中发生的概率均为 ,那么 在这 次试验中恰好发生 次的概率为

例题

  • P31：独立性证明

    • 设 ，证明事件 和 相互独立的充要条件为：

  • P34：Polyá 罐子模型

    • 设罐中有 个红球和 个黑球，随机取出一个球后放回，并加入 个与取出球同色的球，然后进行下一次取球。重复此过程共 次，证明第 次取球时取出红球的概率为 。
    • 要点：使用归纳法证明概率在每次取球后保持不变。

  • ​image​

  • P36：划分事件的概率

    • 设 是样本空间 的一个划分，且 。求事件 比 先发生的概率。
    • 答案：

  • 错排问题

    • 全错排数的通项公式

      • 初值：
      • 递推公式：
      • 推导得
      • 全部排错的概率为：

    • 部分错排即 个里面 个排对了

      • 通项公式：
      • 部分排错的概率为：

‍